회귀분석
- 주어진 데이터로 함수를 만들고 그래프의 기울기와 패턴을 찾는 것
- 회귀 : 기울기
- 분산 : 데이터가 흩어진 정도
- 함수에 fitting할때 잔차가 최소화 되도록 함수를 조정
: fitting = 기대 값에 맞게 결과 값이 나오도록 오차를 줄이는 것
: 잔차 = 데이터 끼리의 거리
: 일반적으로 최소 제곱법을 많이 사용
선형회귀분석
- 비용함수를 최소화하는 가중치와 편향을 찾는 선형적인 회귀(기울기)를 분석하는 것
- 선형 : 그래프의 모양이 일정한 형태
비용함수 그래프 파이썬 예제
import tensorflow as tf # 머신러닝을 위한 라이브러리
import matplotlib.pyplot as plt # 그래프를 그리기 위한 라이브러리
X = tf.constant([1,2,3,4,5], dtype=tf.float32) # 입력 데이터 X (float32 형태의 상수 벡터)
Y = tf.constant([1,2,3,4,5], dtype=tf.float32) # 입력 데이터 Y (float32 형태의 상수 벡터)
def run(W): # 입력 데이터에 대한 연산 (가중치를 매개변수로 받음)
hypothesis = W * X # 가설 값 = 가중치 * X
cost = tf.reduce_mean(tf.square(hypothesis - Y)) # cost = (가설 값 - Y)의 제곱(square)의 차원을 제거하고 평균을 구한 값
return cost.numpy() # cost(비용 값)을 numpy() 함수로 출력
W_val = [] # 가중치 배열
cost_val = [] # 비용 값 배열
for i in range(-30, 50):
w = i * 0.1
c = run(w) # -30부터 50까지 1씩 증가하는 값을 run() 함수의 가중치로 실행
if i%10 == 0: # i가 10으로 나뉘어 질 때 가중치와 비용 값을 출력
print('w = ', w, 'c = ', c)
W_val.append(w) # 가중치 배열과 비용 값 배열에 가중치와 비용 값 추가
cost_val.append(c)
plt.plot(W_val, cost_val) # X축에 가중치 배열을, Y축에 비용 값 배열을 기준으로한 그래프 생성
plt.show() # 그래프 출력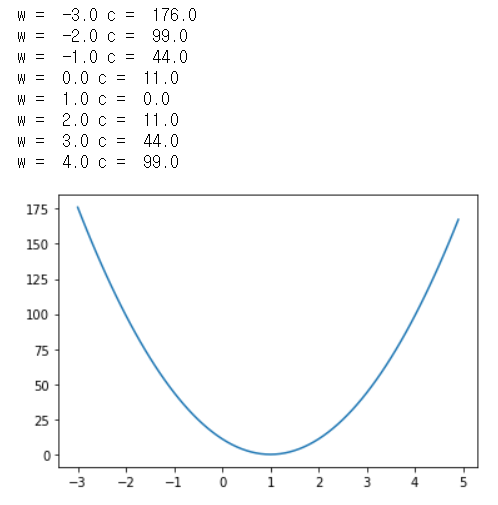
- 출력결과를 보면 가중치의 증가에 따른 비용 값의 변화를 알 수 있다. 아래 그래프는 그러한 추이를 나타낸 것.
여기서 기울기가 가장 낮은 지점은 값의 변화도가 낮은 그래프의 중앙 지점(X축의 1에 가까운 지점)이다.
경사 하강 알고리즘 에서는 시작점 (그래프에서 -3 혹은 5)에서 부터 반대쪽으로 점을 옮겨가며 기울기가
가장 낮아지는 지점을 찾아 그 지점에 해당하는 가중치를 최적 값으로 선정하여 출력한다.
선형회귀 파이썬 구현
# 9장 선형회귀
import tensorflow as tf
# 데이터 정의
x_data = [1,2,3,4,5]
y_data = [1,2,3,4,5]
W = tf.Variable(tf.random.normal([1]), name='Weight') # 가중치 정의 (1,1) 형식의 난수
B = tf.Variable(tf.random.normal([1]), name='Bias') # 편향 정의 (1,1) 형식의 난수
# tf.function을 사용하면 그래프 출력시 성능 향상
# 가설정의
@tf.function
def Hypothesis(X): # 가설정의 (매개변수 = 데이터 값)
return W*X+B # 가중치 * 데이터 값 + B를 출력
# 비용함수(손실함수) 정의
@tf.function
def loss(H,Y): # 가설 값과 Y값을 매개변수로 정의
return tf.reduce_mean(tf.square(H-Y)) # 손실함수 정의 (MSE - 평균제곱오차)
# 손실 값(오차) 출력
# 훈련함수 정의
@tf.function
def train(X, Y, learning_rate=0.01):
with tf.GradientTape() as tape: # 연산의 기울기를 테이프에 기록 (tf.GradientTape())
_loss = loss(Hypothesis(X), Y) # 손실함수를 실행하여 손실 값 입력
_w, _b = tape.gradient(_loss, [W,B]) # 손실 값과 가중치 및 편향의 벡터의 기울기를 변수에 입력
W.assign_sub(learning_rate * _w) # 가중치 - (학습률 * 조정된 가중치) => 오차 반영
B.assign_sub(learning_rate * _b) # 편향 - (학습률 * 조정된 편향) => 오차 반영
# 충분한 훈련 반복
for step in range(2001): # 오차역전법을 통한 모델 훈련 반복
train(x_data, y_data, learning_rate=0.01)
_c = loss(Hypothesis(x_data), y_data)
if step % 20 == 0: # 훈련횟수가 20에 나뉘어질 경우 훈련횟수에 따른 비용 값, 가중치, 편향 값을 출력
print(f"{step} : {_c.numpy()} {W.numpy()} {B.numpy()}")
print('\nfinal w =',W.numpy(), 'b =',B.numpy())
# 테스트
#test data
test_data = [2,4,1,5,3] # 테스트 데이터를 통해 모델의 성능을 테스트
for data in test_data:
y = data * W.numpy() + B.numpy()
print("X =", data, "then Y =",y)

- 훈련횟수 : 비용값 [가중치] [편향]
최종 값 가중치 = 0.9998101 편향 = 0.00068568
※ 파이썬 데코레이터 (@ft.function)
: 파이썬 코드의 일부를 높은 성능의 텐서플로 그래프 코드로 변환
: GPU 혹은 TPU(Tensorflow Processing Unit)을 이용하여 더욱 빠른 연산 실행
'Computer Science > DeepLearning' 카테고리의 다른 글
| 머신러닝 기초 5 - Classification (분류) (0) | 2020.12.16 |
|---|---|
| 머신러닝 기초 4 - 다중 선형회귀 (0) | 2020.12.10 |
| 머신러닝 기초 2 - 머신러닝과 학습 / 학습을 위한 최적화 이론 (0) | 2020.12.10 |
| 머신러닝 기초 1 - 머신러닝의 기초 개념과 신경망 (0) | 2020.12.10 |
| 인공지능 기초 10 - 학습방법과 학습모델 (0) | 2020.12.10 |